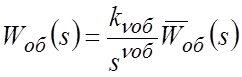что такое астатическая система что такое порядок астатизма

14.12.202323.09.2023 admin 0 Comments

Подскажите : Основы теории управления. Что такое астатизм?

Понятие астатизма является базовым в теории линейных систем управления. Система именуется астатической по отношению к некоторому возмущению, если изменение ее выхода асимптотически стремится к нулю при изменении возмущения на любую постоянную величину. Если выходом является ошибка управления, то астатизм эквивалентен асимптотической инвариантности системы по отношению к постоянным возмущениям. Это свойство, как правило, является желательным, и его наличие в рамках линейной теории легко проверить: передаточная функция от возмущения к выходу должна быть устойчивой, а ее числитель должен иметь нулевой корень. Стандартным способом обеспечения этого свойства является введение интегральной обратной связи. Напомним также, что для линейных систем свойство астатизма влечет за собой ограниченность реакции системы на линейно растущее возмущение.
Представляет интерес распространить понятие астатизма на нелинейные системы, выяснить возможности интегральной обратной связи для обеспечения астатизма и установить, гарантирует ли астатизм ограниченность реакции на возмущение с постоянной или ограниченной скоростью роста. Это и является основной целью данной работы.

Понятие астатизма, традиционное в линейной теории, распространено на нелинейные системы. Приведены условия, при которых обеспечивается астатизм. Рассмотрена проблема реакции нелинейной астатической системы на переменные, но возрастающие с ограниченной скоростью возмущения, а также дана оценка ошибки слежения за изменяющимся желаемым состоянием. Показано, как интегральная обратная связь может обеспечить астатизм. Этот результат использован для анализа управления Лагранжевыми системами.

Основу анализа составляет аппарат функций Ляпунова. Конструктивные выводы появляются, если удается построить соответствующие функции. В качестве примера таких классов систем рассматриваются управляемые Лагранжевы системы, где естественно строятся функции Ляпунова энергетического типа.

Источник

Величина, показывающая отношение ускорения регулируемой координаты к ошибке в установившемся режиме, называется добротностью САР по ускорению, которая численно равна коэффициенту усиления разомкнутой САР:

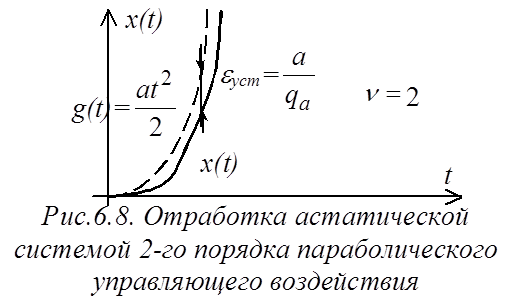
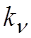
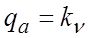
Термин добротность системы по скорости применяется к астатическим системам 1-го порядка, а термин добротность системы по ускорению – к астатическим системам второго порядка.

В обоих случаях, чем выше добротность q, тем меньше установившаяся ошибка 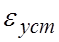, и тем точнее отработка системой управляющего воздействия.

Выше уже отмечалось, что для систем стабилизации, помимо астатизма по управлению (как и в системах точного воспроизведения), важным является решение вопроса астатизма САР по возмущающему воздействию. Если возмущающее воздействие влияет на регулируемую координату в установившемся режиме, САР считается статической по возмущению, в противном случае – астатической.

Структурная схема системы стабилизации представлена на рис.6.9.

Для определения влияния возмущения необходимо сначала найти ПФ САР от возмущения к выходу. Приравниваем g(s)=0 и, считая цепь со звеньями и отрицательной ОС по отношению к возмущению, находим:

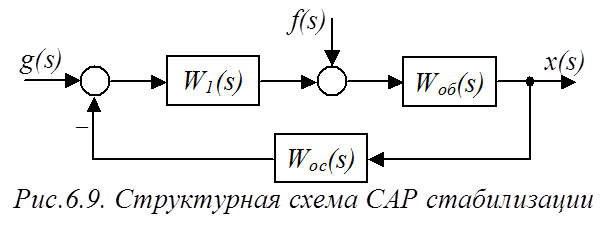
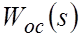
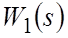
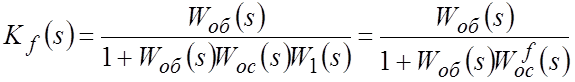
где 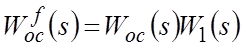– ПФ цепи ОС по отношению к возмущающему воздействию.

Представим ПФ в знаменателе последнего выражения в виде:

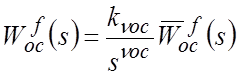
где 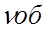– порядок астатизма ПФ ОУ;

– порядок астатизма ПФ цепи ОС по отношению к возмущающему воздействию;

, – соответствующие нормированные ПФ.

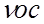
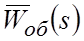
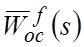
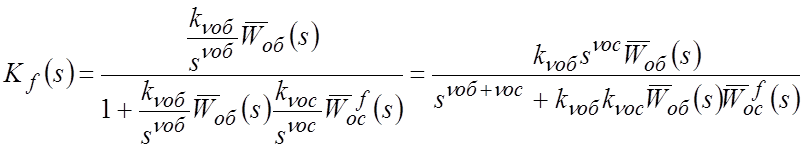
Для исключения влияния возмущения на регулируемую координату (то есть, для обеспечения астатизма САР по возмущению) необходимо, чтобы 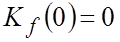. Из последнего выражения следует, что для этого необходимо, чтобы .

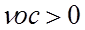
Астатизм САР по возмущающему воздействию определяется порядком астатизма цепи ОС по отношению к возмущению и не зависит от порядка астатизма ОУ. Другими словами, если чистые интеграторы отсутствуют в цепи ОС, то система будет статической, независимо от того, есть ли интеграторы в ОУ или нет.

Пример 1. Определить, является ли система (рис.6.10) астатической по управляющему и возмущающему воздействиям?

Решение. Находим ПФ разомкнутой САР:

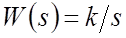
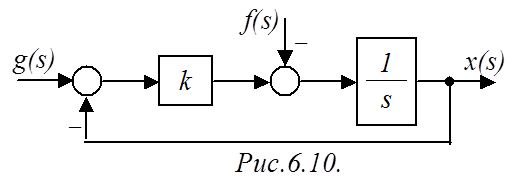
Таким образом, 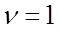, следовательно, по отношению к управляющему воздействию система астатическая 1-го порядка.

Находим ПФ цепи отрицательной ОС по отношению к возмущению:

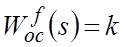
Таким образом, 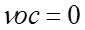, следовательно, система является статической по отношению к возмущающему воздействию.

Пример 2. Определить, является ли система (рис.6.11) астатической по управляющему и возмущающему воздействиям?

Решение. Находим ПФ разомкнутой САР:

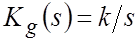
Таким образом, 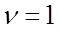, следовательно, по отношению к управляющему воздействию система астатическая 1-го порядка.

Находим ПФ цепи отрицательной ОС по отношению к возмущению:

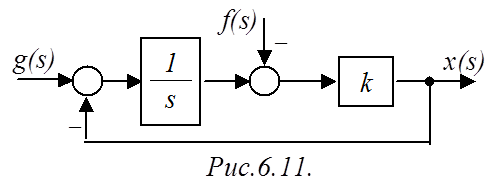
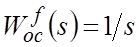
Таким образом, 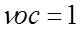, следовательно, и по отношению к возмущающему воздействию система является астатической 1-го порядка.

Уравнения и передаточные функции системы

«силовой преобразователь – двигатель»

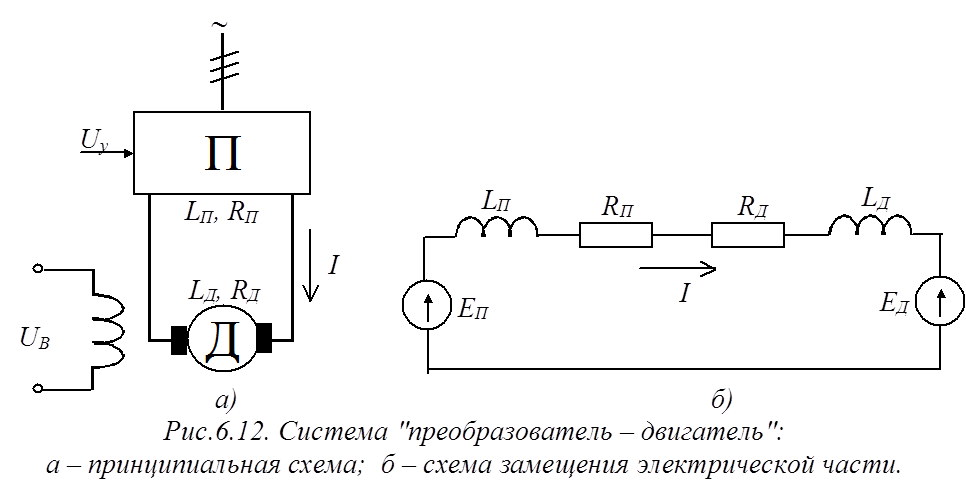
Принципиальная схема система «преобразователь – двигатель» представлена на рис.6.12а.

Тиристорный преобразователь П предназначен для выпрямления сетевого трехфазного напряжения, на его выходе имеем выпрямленное ЭДС преобразователя E_П, величина которого зависит от значения напряжения управления U_y. Электромагнитные свойства преобразователя характеризуются активным сопротивлением R_П и индуктивностью L_П.

ЭДС, наводимая в обмотке якоря двигателя E_Д направлена встречно с ЭДС преобразователя E_П и пропорциональна частоте вращения вала двигателя. Индуктивность и активное сопротивление цепи якоря двигателя Д

; ,

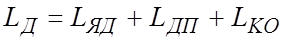
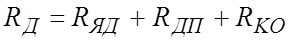
где 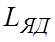, – параметры цепи собственно якоря двигателя; , – параметры обмотки добавочных полюсов; , – параметры компенсационной обмотке.

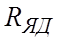
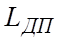
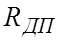
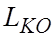
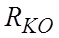
Электрическая схема замещения электрической части системы «преобразователь – двигатель» представлена на рис.6.12б.

; ,

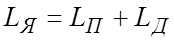
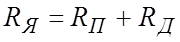
дифференциальное уравнение электрического равновесия цепи якоря запишем в следующем виде:

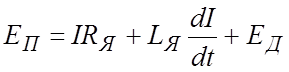
Соответствующее уравнение в изображениях Лапласа:

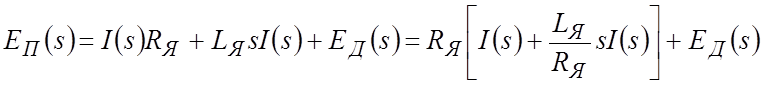
Обозначим 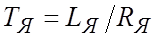– электромагнитная постоянная времени силовой цепи якоря двигателя, с. Тогда последнее уравнение запишется в виде:

. (1)

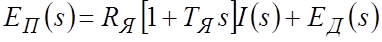
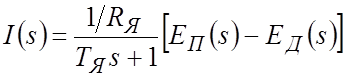
ЭДС двигателя пропорциональна частоте вращения вала:

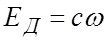
или, переходя к изображениям Лапласа,

, (2)

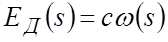
где 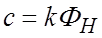– конструктивная постоянная, пропорциональная номинальному магнитному потоку двигателя.

Наконец, уравнение механического равновесия

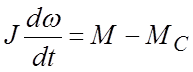
где M – электромагнитный момент, развиваемый двигателем; M_C – момент статического сопротивления (нагрузки); J – суммарный момент инерции вала двигателя.

Уравнение электромагнитного момента имеет вид:

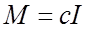
и формально статический момент может быть представлен в аналогичном виде:

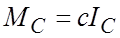
где 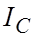– ток статической нагрузки.

С учетом этого уравнение механического равновесия может быть представлено в виде:

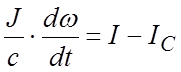
Переходя к изображениям Лапласа:

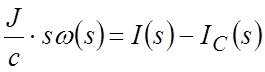
после преобразований получим:

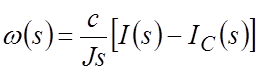
Вводя понятие электромеханической постоянной времени 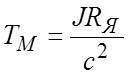, последнее уравнение представим в окончательном виде:

. (3)

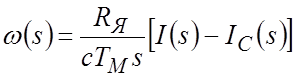
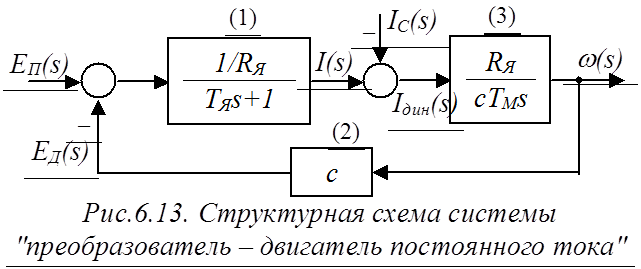
Уравнениям (1) – (3) соответствует структурная схема, представленная на рис.6.13.

Анализируя структурную схему (рис.6.13), можно увидеть, что данная система астатическая по отношению к управляющему воздействию E_П(s) (поскольку присутствует чистый интегратор в блоке (3)), и в то же время статическая по отношению к возмущающему воздействию I_C(s) (в блоках (1) и (2) отсутствуют интеграторы). Таким образом, при изменении нагрузки I_C на валу двигателя будет изменяться и скорость w(s).

ПФ по управляющему воздействию:

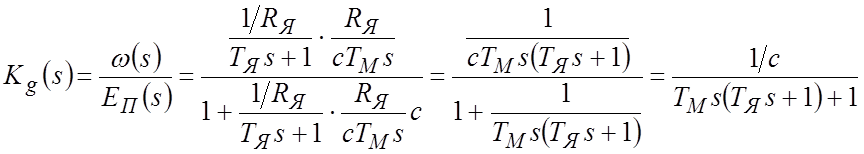
В установившемся режиме

, и .

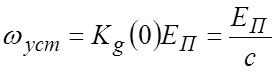
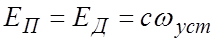
ПФ по возмущающему воздействию:

Т.е., при подаче какого-то управляющего воздействия (рис.6.14) двигатель каким-то образом (показано пунктирной линией) разгонится до скорости . После скачкообразного приложения возмущающего воздействия (наброса нагрузки) будет иметь место ошибка регулирования, которая после затухания переходного процесса будет равна .

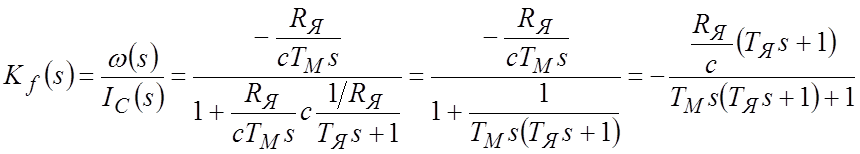
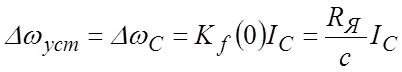
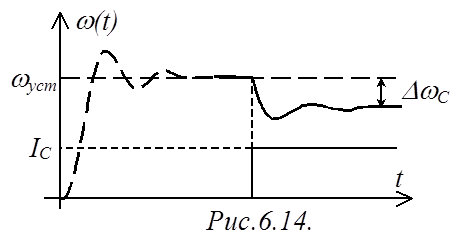
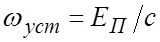
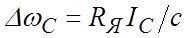
Сравнивая ПФ 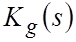и , видим, что знаменатели, т.е., характеристические полиномы двигателя, остаются одинаковыми вне зависимости от того, что является входом, и что – выходом.

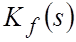
Этот вывод можно распространить на любую замкнутую САР: характеристический полином 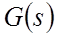не зависит от того, на основании какой ПФ он записан.

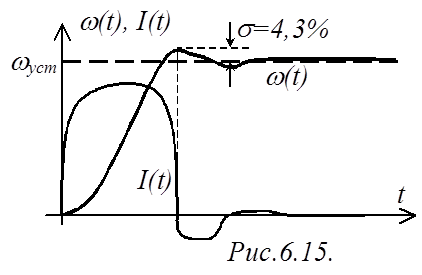
Для определения характера переходного процесса при подаче управляющего воздействия рассмотрим детальней ПФ :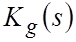

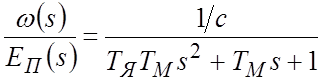
Таким образом, если 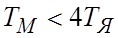, будем иметь колебательное звено, если же , то данная ПФ является ПФ двух последовательно соединенных апериодических звеньев.

Например, при и переходный процесс по току и скорости качественно будет иметь вид, показанный на рис.6.15. Отметим, что точки экстремума кривой w(t) совпадают по времени с нулевыми значениями I(t), поскольку ток, согласно (3), является производной от скорости.

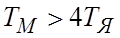
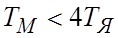
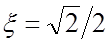
Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Астатическая система регулирования

Полезное

Смотреть что такое «Астатическая система регулирования» в других словарях:

АСТАТИЧЕСКАЯ САР — система регулирования автоматического, содержащая астатический регулятор. Примером может служить система автоматич. регулирования уровня жидкости (см. рис.): при увеличении (уменьшении) расхода жидкости поплавок перемещается и замыкает верхний… … Большой энциклопедический политехнический словарь

СИСТЕМА АСТАТИЧЕСКАЯ — система автоматического (см.), обладающая (см.) свойством сводить к нулю установившиеся ошибки регулирования или слежения, возникающие под влиянием управляющих или возмущающих воздействий … Большая политехническая энциклопедия

Регулирование автоматическое — (от нем. regulieren регулировать, от лат. regula норма, правило) поддержание постоянства (стабилизация) некоторой регулируемой величины, характеризующей технический процесс, либо её изменение по заданному закону (программное… … Большая советская энциклопедия

Регулятор — автоматический (от лат. regulo привожу в порядок, налаживаю), устройство (совокупность устройств), посредством которого осуществляется Регулирование автоматическое. С помощью чувствительного элемента Датчика Р. в зависимости от принципа… … Большая советская энциклопедия

СТАТИЧЕСКАЯ САР — система регулирования автоматического, содержащая статический регулятор. Примером может служить система регулирования уровня жидкости в сосуде (см. рис.).: при увеличении (уменьшении) расхода жидкости поплавок перемещается и задвижка поднимается… … Большой энциклопедический политехнический словарь

Источник

Что такое астатическая система что такое порядок астатизма

Повышение точности САУ увеличением порядка астатизма основывается главным образом на введении в систему дополнительных интегрирующих или изодромных устройств. Последовательное включение интегрирующих устройств с передаточной функцией

в канал усиления системы непосредственно приводит к повышению порядка астатизма и, следовательно, к снижению установившихся

ошибок. Однако при этом снижается запас устойчивости системы или вообще система оказывается неустойчивой.

Повышение порядка астатизма с целью увеличения точности без неблагоприятного влияния на устойчивость может быть достигнуто включением изодромных устройств, представляющих собой совокупность двух параллельно включенных звеньев — идеального интегрирующего и безынерционного. Передаточная функция изодромного устройства

где — постоянная времени изодромного устройства.

Сравнить рассмотренные способы повышения порядка астатизма можно на примере следящей системы, передаточная функция которой соответствует астатизму первого порядка и имеет вид (рис. 6.1, а)

Коэффициенты ошибки для этой исходной системы равны (см. § 5.6):

При введении интегрирующего устройства (рис. 6.1, б) передаточная функция разомкнутой системы приобретает вид

где — общий коэффициент усиления по ускорению.

Передаточная функция (6.8) соответствует уже системе с астатизмом второго порядка. Передаточная функция замкнутой системы по ошибке

Коэффициенты ошибки легко получаются разложением

Рис. 6.1. Структурные схемы следящей системы: а — исходная; б — с интегрирующим устройством; в — с изодромным устройством

выражения (6.9) в ряд путем деления многочлена числителя на многочлен знаменателя:

Так как , то скоростная ошибка обращается в нуль. Однако оказывается, что полученная система вообще является неработоспособной, так как не выполняется необходимое условие устойчивости. В характеристическом уравнении отсутствует коэффициент при первой степени Действительно, характеристическое уравнение имеет

При введении изодромного устройства (рис. 6.1, в) передаточная функция разомкнутой системы

Передаточная функция замкнутой системы по ошибке

Коэффициенты ошибки имеют вид

Сравнение (6.14) с (6.10) показывает, что применение изодромного устройства снижает коэффициент что благоприятно сказывается на точности системы. Однако главное состоит в том, что в этом случае систему можно сделать устойчивой. Характеристическое уравнение замкнутой системы запишется следующим образом: