что такое арифметическая прогрессия и как ее решать
Арифметическая прогрессия
Арифметической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего прибавлением к нему постоянного числа. Это число называют разностью арифметической прогрессии и обозначают буквой \(d\).
Например, последовательность \(2\); \(5\); \(8\); \(11\); \(14\)… является арифметической прогрессией, потому что каждый следующий элемент отличается от предыдущего на три (может быть получен из предыдущего прибавлением тройки):
В этой прогрессии разность \(d\) положительна (равна \(3\)), и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими.
Однако \(d\) может быть и отрицательным числом. Например, в арифметической прогрессии \(16\); \(10\); \(4\); \(-2\); \(-8\)… разность прогрессии \(d\) равна минус шести.
И в этом случае каждый следующий элемент будет меньше, чем предыдущий. Эти прогрессии называются убывающими.
Обозначение арифметической прогрессии
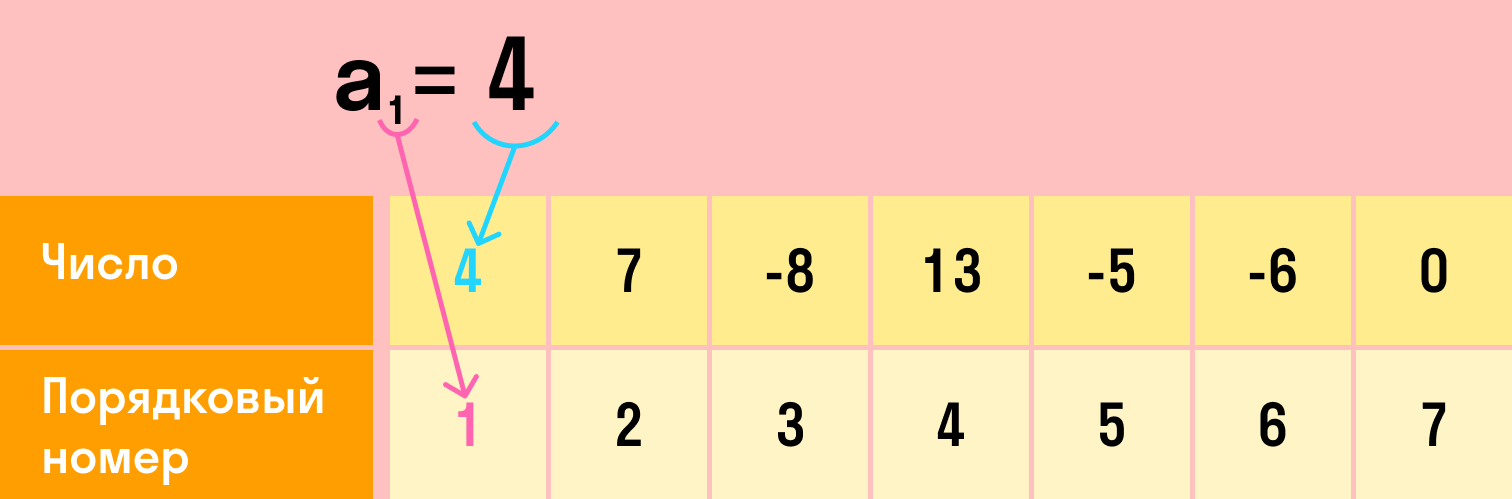
Прогрессию обозначают маленькой латинской буквой.
Числа, образующие прогрессию, называют ее членами (или элементами).
Их обозначают той же буквой что и арифметическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.
Например, арифметическая прогрессия \(a_n = \left\< 2; 5; 8; 11; 14…\right\>\) состоит из элементов \(a_1=2\); \(a_2=5\); \(a_3=8\) и так далее.
Иными словами, для прогрессии \(a_n = \left\<2; 5; 8; 11; 14…\right\>\)
| порядковый номер элемента | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| обозначение элемента | \(a_1\) | \(a_2\) | \(a_3\) | \(a_4\) | \(a_5\) |
| значение элемента | \(2\) | \(5\) | \(8\) | \(11\) | \(14\) |
Решение задач на арифметическую прогрессию
В принципе, изложенной выше информации уже достаточно, чтобы решать практически любую задачу на арифметическую прогрессию (в том числе из тех, что предлагают на ОГЭ).
Пример (ОГЭ). Арифметическая прогрессия задана условиями \(b_1=7; d=4\). Найдите \(b_5\).
Решение:
В этой задаче нам дано начало цепочки (первый элемент) и шаг (разность). Зная их, мы легко можем восстановить прогрессию до любого нужного нам члена (в нашем случае – пятого).
Вот и все. Нужное нам значение найдено.
Пример (ОГЭ). Даны первые три члена арифметической прогрессии: \(62; 49; 36…\) Найдите значение первого отрицательного члена этой прогрессии..
Решение:
Нам даны первые элементы последовательности и известно, что она – арифметическая прогрессия. То есть, каждый элемент отличается от соседнего на одно и то же число. Узнаем на какое, вычтя из следующего элемента предыдущий: \(d=49-62=-13\).
Теперь мы можем восстановить нашу прогрессию до нужного нам (первого отрицательного) элемента.
Готово. Можно писать ответ.
Пример (ОГЭ). Даны несколько идущих подряд элементов арифметической прогрессии: \(…5; x; 10; 12,5. \) Найдите значение элемента, обозначенного буквой \(x\).
Решение:
Чтоб найти \(x\), нам нужно знать на сколько следующий элемент отличается от предыдущего, иначе говоря – разность прогрессии. Найдем ее из двух известных соседних элементов: \(d=12,5-10=2,5\).
А сейчас без проблем находим искомое: \(x=5+2,5=7,5\).
Готово. Можно писать ответ.
Пример (ОГЭ). Арифметическая прогрессия задана следующими условиями: \(a_1=-11\); \(a_
Решение:
Нам нужно найти сумму первых шести членов прогрессии. Но мы не знаем их значений, нам дан только первый элемент. Поэтому сначала вычисляем значения по очереди, используя данное нам рекуррентное соотношение :
Искомая сумма найдена.
Пример (ОГЭ).В арифметической прогрессии \(a_<12>=23\); \(a_<16>=51\). Найдите разность этой прогрессии.
Решение:
Подставляем известные величины.
Вычисляем правую часть…
Важные формулы арифметической прогрессии
Как видите, многие задачи по арифметической прогрессии можно решать, просто поняв главное – то, что арифметическая прогрессия есть цепочка чисел, и каждый следующий элемент в этой цепочке получается прибавлением к предыдущему одного и того же числа (разности прогрессии).
Однако порой встречаются ситуации, когда решать «в лоб» весьма неудобно. Например, представьте, что в самом первом примере нам нужно найти не пятый элемент \(b_5\), а триста восемьдесят шестой \(b_<386>\). Это что же, нам \(385\) раз прибавлять четверку? Или представьте, что в предпоследнем примере надо найти сумму первых семидесяти трех элементов. Считать замучаешься…
Поэтому в таких случаях «в лоб» не решают, а используют специальные формулы, выведенные для арифметической прогрессии. И главные из них это формула энного члена прогрессии и формула суммы \(n\) первых членов.
Формула \(n\)-го члена: \(a_n=a_1+(n-1)d\), где \(a_1\) – первый член прогрессии;
\(n\) – номер искомого элемента;
\(d\) – разность прогрессии;
\(a_n\) – член прогрессии с номером \(n\).
Эта формула позволяет нам быстро найти хоть трехсотый, хоть миллионный элемент, зная только первый и разность прогрессии.
Пример. Арифметическая прогрессия задана условиями: \(b_1=-159\); \(d=8,2\). Найдите \(b_<246>\).
Решение:
Больше двухсот раз прибавлять \(8,2\) к \(-159\) – перспектива не самая радужная. Лучше воспользуемся формулой, подставив вместо \(n\) номер искомого элемента.
Можно писать ответ.
Формула суммы n первых членов: \(S_n=\frac <2>\cdot n\), где
\(S_n\) – искомая сумма \(n\) первых элементов;
\(a_1\) – первый суммируемый член;
\(a_n\) – последний суммируемый член;
\(n\) – количество элементов в сумме.
Пример (ОГЭ).Арифметическая прогрессия задана условиями \(a_n=3,4n-0,6\). Найдите сумму первых \(25\) членов этой прогрессии.
Решение:
Чтобы вычислить сумму первых двадцати пяти элементов, нам нужно знать значение первого и двадцать пятого члена.
Наша прогрессия задана формулой энного члена в зависимости от его номера (подробнее смотри здесь ). Давайте вычислим первый элемент, подставив вместо \(n\) единицу.
Теперь найдем двадцать пятый член, подставив вместо \(n\) двадцать пять.
Ну, а сейчас без проблем вычисляем искомую сумму.
Для суммы \(n\) первых членов можно получить еще одну формулу: нужно просто в \(S_<25>=\) \(\frac
Формула суммы n первых членов: \(S_n=\) \(\frac<2a_1+(n-1)d><2>\) \(\cdot n\), где
\(S_n\) – искомая сумма \(n\) первых элементов;
\(a_1\) – первый суммируемый член;
\(d\) – разность прогрессии;
\(n\) – количество элементов в сумме.
Для решения задачи воспользуемся последней формулой. Первый элемент известен, нужно найти только разность прогрессии \(d\). Вычисляем ее как разность двух соседних элементов.
Теперь можно посчитать сумму \(33\)-ех элементов.
Готово. Быстро и просто, почти как Доширак. Но гораздо менее вредно.
Более сложные задачи на арифметическую прогрессию
Теперь у вас есть вся необходимая информация для решения практически любой задачи на арифметическую прогрессию. Завершим тему рассмотрением задач, в которых надо не просто применять формулы, но и немного думать (в математике это бывает полезно ☺)
Пример (ОГЭ).Найдите сумму всех отрицательных членов прогрессии: \(-19,3\); \(-19\); \(-18,7\)…
Решение:
Задача очень похожа на предыдущую. Начинаем решать также: сначала найдем \(d\).
Теперь бы подставить \(d\) в формулу для суммы… и вот тут всплывает маленький нюанс – мы не знаем \(n\). Иначе говоря, не знаем сколько членов нужно будет сложить. Как это выяснить? Давайте думать. Мы прекратим складывать элементы тогда, когда дойдем до первого положительного элемента. То есть, нужно узнать номер этого элемента. Как? Запишем формулу вычисления любого элемента арифметической прогрессии: \(a_n=a_1+(n-1)d\) для нашего случая.
Нам нужно, чтоб \(a_n\) стал больше нуля. Выясним, при каком \(n\) это произойдет.
Делим обе части неравенства на \(0,3\).
Переносим минус единицу, не забывая менять знаки
…и выясняется, что первый положительный элемент будет иметь номер \(66\). Соответственно, последний отрицательный имеет \(n=65\). На всякий случай, проверим это.
Таким образом, нам нужно сложить первые \(65\) элементов.
Пример (ОГЭ).Арифметическая прогрессия задана условиями: \(a_1=-33\); \(a_
Решение:
Для нашей прогрессии \(a_1=-33\), а разность \(d=4\) (ведь именно четверку мы добавляем к предыдущему элементу, чтоб найти следующий). Зная это, найдем сумму первых \(42\)-ух элементов.
Теперь сумму первых \(25\)-ти элементов.
Ну и наконец, вычисляем ответ.
Арифметическая прогрессия свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
«Последовательность простых чисел: 4, 6, 10, 19, 21, 33. »
Последовательность yn = C называют постоянной или стационарной.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
Возрастающие и убывающие последовательности называют монотонными последовательностями.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2. a10. an.
N-ый член последовательности можно задать формулой. Например:
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.
















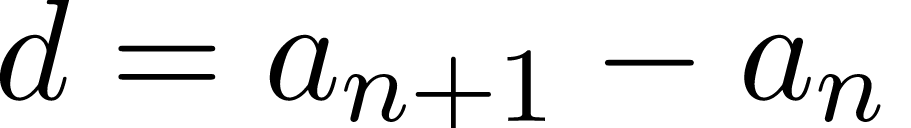
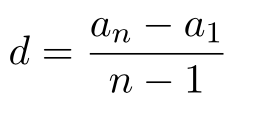
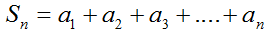
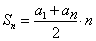
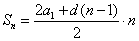

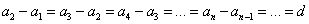
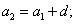
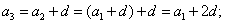
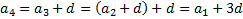
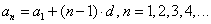
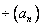
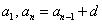

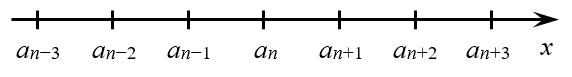 Члены арифметической прогрессии на числовой прямой
Члены арифметической прогрессии на числовой прямой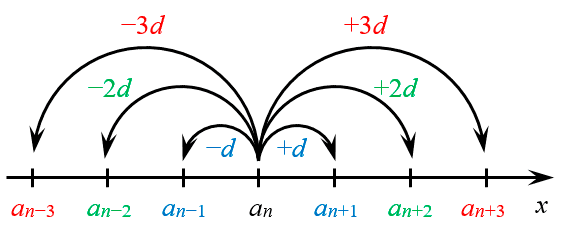 Члены прогрессии лежат на одинаковом расстоянии от центра
Члены прогрессии лежат на одинаковом расстоянии от центра На числовой прямой отмечены 6 элементов
На числовой прямой отмечены 6 элементов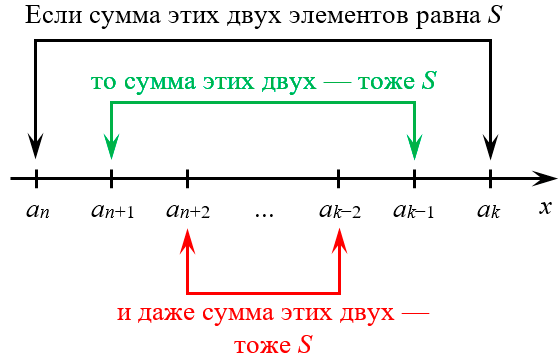 Одинаковые отступы дают равные суммы
Одинаковые отступы дают равные суммы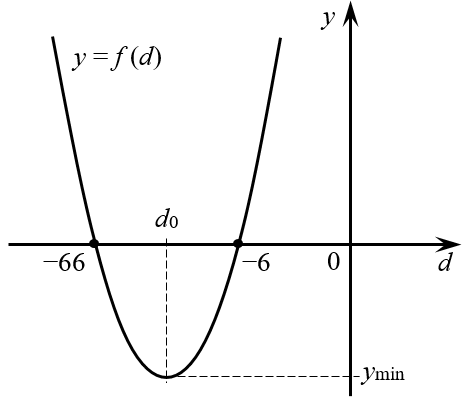 график квадратичной функции — парабола
график квадратичной функции — парабола