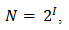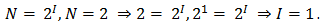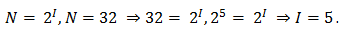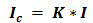что такое алфавитный подход к измерению информации

Измерение информации. Алфавитный подход к измерению информации. Мощность алфавита. Информационный объем текста

Алфавитный подход к измерению информации Вам хорошо известно, что для измерения таких величин, как, например, расстояние, масса, время, существуют эталонные единицы. Для расстояния — это метр, для массы — килограмм, для времени — секунда. Измерение происходит путем сопоставления измеряемой величины с эталонной единицей. Сколько раз эталонная единица укладывается в измеряемой величине, таков и результат измерения. Следовательно, и для измерения информации должна быть введена своя эталонная единица. Алфавитный подход позволяет измерять информационный объем текста на некотором языке (естественном или формальном), не связанный с содержанием этого текста.

Алфавит. Мощность алфавита
Под алфавитом мы будем понимать набор букв, знаков препинания, цифр, скобок и др. символов, используемых в тексте. В алфавит также следует включить и пробел, т. е. пропуск между словами.
Полное число символов в алфавите принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54:33 буквы + 10 цифр + 11 знаков препинания, скобки, пробел.

Информационный вес символа
При алфавитном подходе считается, что каждый символ текста имеет определенный информационный вес. Информационный вес символа зависит от мощности алфавита. А каким может быть наименьшее число символов в алфавите? Оно равно двум! Скоро вы узнаете, что такой алфавит используется в компьютере. Он содержит всего 2 символа, которые обозначаются цифрами «0» и «1». Его называют двоичным алфавитом. Изучая устройство и работу компьютера, вы узнаете, как с помощью всего двух символов можно представить любую информацию.

Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.

Источник

Что такое алфавитный подход к измерению информации

Каким образом в этом случае можно найти количество информации?

канал передачи информации

Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению коли­чества информации).
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель зара­нее точно знает, какой знак придет, то полученное ко­личество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его ин­формационная емкость.
В русской письменной речи частота использования букв в тексте различна, так в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в сто раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, инфор­мационная емкость знаков русского алфавита различ­на (у буквы «а» она наименьшая, а у буквы «ф» — наибольшая).
Количество информации в сообщении. Сообщение состо­ит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации Iс в сообщении можно подсчитать, умножив количество информации I3, которое несет один знак, на длину кода (количество знаков в сообщении) К:

Информация и информационные процессы

Так, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут ин­формацию в 2 бита, три цифры — в 3 бита и т. д. Количест­во информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.3).
Количество информации, которое несет двоич­ный компьютерный код.

Двоичный компьютерный код

Символов на нашей клавиатуре около 200 (русский и латинский алфавит, строчные и прописные буквы, цифры, знаки препинания, спецсимволы). Попробуем подобрать число n, достаточное для кодирования этих символов: 27 = 128 (мало), 28 = 256 (хватит). Поэтому в кодировке ASCII 1 символ текста кодируется одним байтом (8 битами).

Количество данных, обрабатываемых компьютером, измеряется в байтах, но чаще для этого используются более крупные единицы:
1 Килобайт (Кб) = 2 10 байт = 1024 байт
1 Мегабайт (Мб) = 2 10 Кб = 1 048 576 байт
1 Гигабайт (Гб) = 2 10 Мб = 1 073 741 824 байт.

Скорость передачи данных и пропускную способность каналов связи принято измерять в битах в секунду (бит/с) и кратных этому:
1 килобит (кбит/с) = 10 3 бит/с
1 мегабит (мбит/с) = 10 6 бит/с
1 гигабит (гбит/с) = 10 9 бит/с
А при измерении оперативной памяти принято измерение в единицах, кратных не степеням десятки, а степеням двойки.

Из-за этого первоначально и возникла путаница в приставках.

Источник

Алфавитный подход к определению количества информации

Цели урока:

1) Обучающая: рассмотреть алфавитный подход к измерению количества информации, научиться вычислять количество информации с точки зрения алфавитного подхода.

2) Развивающая: развитие у учащихся самостоятельности и познавательной активности.

3) Воспитывающая: воспитывать дисциплинированность, аккуратность, собранность.

Литература:

1) Угринович Н. Д. «Информатика 8 класс»,

2) Заславская О. Ю., Левченко И. В. «Информатика: весь курс».

1) Угринович Н. Д. «Информатика 8 класс».

Тип урока: ознакомление с новым материалом

План урока:

1. Организационный этап.

2. Актуализация знаний.

3. Подготовка учащихся к усвоению нового материала.

4. Этап получения новых знаний.

5. Этап обобщения и закрепления нового материала.

7. Заключительный этап.

Ход урока

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

1) В чём заключается содержательный подход к измерению информации? (Количество информации — мера уменьшения неопределённости знаний при получении информационных сообщений.)

2) Какую минимальную единицу информации используют для измерения количества информации? (Бит)

3) Какую формулу используют для определения количества информации? (Формулу Хартли)

4) Производится бросание симметричной четырехгранной пирамидки. Какое количество информации мы получаем в зрительном сообщении о ее падении на одну из граней? (2 бита)

6) Из непрозрачного мешочка вынимают шарики с номерами и известно, что информационное сообщение о номере шарика несет 5 битов информации. Определите количество шариков в мешочке. (35)

3. Этап получения новых знаний.

Скачать видеоурок «Алфавитный подход к определению количества информации»

Содержательный подход к измерению информации рассматривает информацию с точки зрения человека, как уменьшение неопределенности наших знаний.

Однако любое техническое устройство не воспринимает содержание информации. Поэтому в вычислительной технике используется другой подход к определению количества информации. Он называется алфавитным подходом.

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.

Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, пропуск между словами.

Алфавит — это множество символов, используемых при записи текста.

Мощность (размер) алфавита — это полное количество символов в алфавите.

Мощность алфавита обозначается буквой N.

· мощность алфавита из русских букв равна 33;

· мощность алфавита из латинских букв — 26;

· мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания );

· мощность двоичного алфавита равна 2.

При алфавитном подходе считается, что каждый символ текста имеет информационную емкость. Информационная емкость знака зависит от мощности алфавита.

Алфавит, с помощью которого записано сообщение состоит из N знаков. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений, которое будет нести количество информации I.

N — количество знаков в алфавите знаковой системы, I — количество информации, которое несет каждый знак.

Например, из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе

Информационная емкость знака двоичной знаковой системы составляет 1 бит.

Задача 1. Определите, какое количество информации несет буква русского алфавита (без буквы ё).

Буква русского алфавита несет 5 битов информации.

Формула 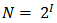связывает между собой количество возможных событий и количество информации, которое несёт полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите, знаковой системы, а I — количество информации, которое несёт один знак.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно посчитать, умножив количество информации, которое несет один знак на количество знаков в сообщении.

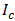
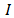
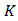
где — количество информации в сообщении

— количество информации, которое несет один знак

— количество знаков в сообщении

Давайте решим с вами задачу.

Задача 2. Какое количество информации содержит слово «ПРИВЕТ», если считать, что алфавит состоит из 32 букв?

Решение. Что нам требуется найти в данной задаче? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».

Что нам для этого дано?

Дано: количество знаков в сообщение и мощность алфавита.

Количество знаков в сообщении равно 6, а мощность данного алфавита равна 32.

Что нам нужно найти? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».

Посмотрим на наше сообщение, оно содержит несколько знаков, значит для того чтобы найти количество информации нашего сообщения, нам нужно умножив количество информации, которое несет один знак, на количество знаков в сообщении, воспользоваться формулой «и» суммарное равно «и» умножить на «к».

Но мы еще не можем воспользоваться формулой, т.к. не знаем какое количество информации несет один знак. Для этого воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна 32, N равно 32. Мы получили уравнение. Решив это уравнение, мы получили, что количество информации, которое несет один знак нашего алфавита, равно 5 бит. Зная количество информации, которое несет один знак нашего алфавита, и количество знаков в сообщении, мы можем найти какое количество информации содержит наше сообщение.

Итак, наше сообщение содержит 30 бит.

4. Этап обобщения и закрепления нового материала.

1) Какое количество информации содержит слово «ИНФОРМАТИКА», если считать, что алфавит состоит из 32 букв? (55 битов)

2) Определить количество информации, содержащееся в слове из 10 символов, если известно, что мощность алфавита равна 32 символам. (50 бит)

3) Сколько бит информации содержится в сообщении, состоящем из 5 символов, при использовании алфавита, состоящего из 64 символов. (6 битов)

4) Определить информативность сообщения «А + В = С», если для описания математических формул необходимо воспользоваться 64-символьным алфавитом. (30 бит)

5) Для представления числовых данных используют 16-ричный алфавит, включающий знаки математических действий. Сколько битов информации содержит выражение «32 * 5 = 160»? (32 бита)

6) Практическая работа № 2. «Тренировка ввода текстовой и числовой информации с помощью клавиатурного тренажера»

5. Рефлексия.

Источник

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

§ 1.6. Измерение информации

Информатика. 7 класса. Босова Л.Л. Оглавление

1.6.1. Алфавитный подход к измерению информации

Одно и то же сообщение может нести много информации для одного человека и не нести её совсем для другого человека. При таком подходе количество информации определить однозначно затруднительно.

Алфавитный подход позволяет измерить информационный объём сообщения, представленного на некотором языке (естественном или формальном), независимо от его содержания.

Для количественного выражения любой величины необходима, прежде всего, единица измерения. Измерение осуществляется путём сопоставления измеряемой величины с единицей измерения. Сколько раз единица измерения «укладывается» в измеряемой величине, таков и результат измерения.

При алфавитном подходе считается, что каждый символ некоторого сообщения имеет определённый информационный вес — несёт фиксированное количество информации. Все символы одного алфавита имеют один и тот же вес, зависящий от мощности алфавита. Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется 1 бит.

Обратите внимание, что название единицы измерения информации «бит» (bit) происходит от английского словосочетания binary digit — «двоичная цифра».

За минимальную единицу измерения информации принят 1 бит. Считается, что таков информационный вес символа двоичного алфавита.

1.6.2. Информационный вес символа произвольного алфавита

Разрядность двоичного кода принято считать информационным весом символа алфавита. Информационный вес символа алфавита выражается в битах.

Задача 1. Алфавит племени Пульти содержит 8 символов. Каков информационный вес символа этого алфавита?

Решение. Составим краткую запись условия задачи.

Полная запись решения в тетради может выглядеть так:

1.6.3. Информационный объём сообщения

Информационный объём сообщения (количество информации в сообщении), представленного символами естественного или формального языка, складывается из информационных весов составляющих его символов.

Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i;I = К • i.

Задача 2. Сообщение, записанное буквами 32-символьного алфавита, содержит 140 символов. Какое количество информации оно несёт?

Задача 3. Информационное сообщение объёмом 720 битов состоит из 180 символов. Какова мощность алфавита, с помощью которого записано это сообщение?

1.6.4. Единицы измерения информации

1 байт = 8 битов

Бит и байт — «мелкие» единицы измерения. На практике для измерения информационных объёмов используются более крупные единицы:

1 килобайт = 1 Кб = 1024 байта = 2 10 байтов
1 мегабайт = 1 Мб = 1024 Кб = 2 10 Кб = 2 20 байтов
1 гигабайт = 1 Гб = 1024 Мб = 2 10 Мб = 2 20 Кб = 2 30 байтов
1 терабайт = 1 Тб = 1024 Гб = 2 10 Гб = 2 20 Мб = 2 30 Кб = 2 40 байтов

Задача 4. Информационное сообщение объёмом 4 Кбайта состоит из 4096 символов. Каков информационный вес символа используемого алфавита? Сколько символов содержит алфавит, с помощью которого записано это сообщение?

Ответ: 8 битов, 256 символов.

Задача 5. В велокроссе участвуют 128 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер цепочкой из нулей и единиц минимальной длины, одинаковой для каждого спортсмена. Каков будет информационный объём сообщения, записанного устройством после того, как промежуточный финиш пройдут 80 велосипедистов?

Ответ: 70 байтов.

Самое главное.

При алфавитном подходе считается, что каждый символ некоторого сообщения имеет опредёленный информационный вес — несёт фиксированное количество информации.

1 бит — минимальная единица измерения информации.

Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i: I = K•i.

Байт, килобайт, мегабайт, гигабайт, терабайт — единицы измерения информации. Каждая следующая единица больше предыдущей в 1024 (210) раза.

Вопросы и задания.

1.Ознакомтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.

Источник

Измерение информации

Всего получено оценок: 397.

Всего получено оценок: 397.

Как и любую другую физическую величину, информацию можно измерить. Существуют разные подходы к измерению информации. Один из таких подходов рассматривается в курсе информатики за 7 класс.

Что такое измерение информации

При измерении информации следует учитывать как объем передаваемого сообщения, так и его смысловую нагрузку. В связи с этим в информатике существуют разные подходы к измерению информации.

Алфавитный подход к измерению информации

Способы оценки величины информации могут учитывать или не учитывать смысла информационного сообщения.

Один из способов нахождения количества информации основан на определении веса каждого символа в тексте сообщения. При таком подходе объем сообщения зависит от количества знаков в тексте, чем больше тест, тем больше весит информационное сообщение. При этом абсолютно не важно, что написано, какой смысл несет сообщение. Так как определение объема информации привязано к текстовым единицам: буквам, цифрам, знакам препинания, то такой подход к измерению информации получил название алфавитного.

Вес отдельного знака зависит от их количества в алфавите. Число символов алфавита называют мощностью (N). Например, мощность алфавита английского языка по числу символов равно 26, русского языка 33. Но на самом деле, при написании текста используются и прописные и строчные буквы, а также знаки препинания, пробелы и специальные невидимые символы, обозначающие конец абзаца и перевод к новой строке. Поэтому имеют дело с мощностью 128 или в расширенной версии 256 символов.

Бит, байт и другие единицы измерения

Для двоичного алфавита, состоящего из двух символов – нуля и единицы, мощность алфавита будет составлять 2. Вес символа бинарного алфавита выбран в качестве минимальной единицы информации и называется «бит». Происхождение термина «бит» исходит от англоязычного слова «binary», что означает двоичный.

Восемь бит образуют байт.

Название «байт» было придумано в 1956 году В. Бухгольцем при проектировании первого суперкомпьютера. Слово «byte» было получено путем замены второй буквы в созвучном слове «bite», чтобы избежать путаницы с уже имеющимся термином «bit».

На практике величина объема информации выражает в более крупных единицах: килобайтах, терабайтах, мегабайтах.

Следует запомнить, что килобайт равен 1024 байта, а не 1000. Как, например, 1 километр равен 1000 метрам. Эта разница получается за счет того, 1 байт равен 8 битам, а не 10.

Для того, чтобы легче запомнить единицы измерения, следует воспользоваться таблицей степени двойки.

Таблица степеней двойки

Показатель степени

Значение

То есть, 2 3 = 8 – это 1 байт, состоящий из 8 бит, 2 10 = 1024 это 1 килобайт, 2 20 = 1048576 представляет собой 1 мегабайт, 2 30 = 1 гигабайт, 2 40 = 1 терабайт.

Определение количества информации

Вес символа (i) и мощность алфавита (N) связаны между собой соотношением: 2 i = N.

Так, алфавит мощностью в 256 символов имеет вес каждого символа в 8 бит, то есть один байт. Это означает, что на каждую букву приходится по байту. В таком случае, нетрудно определить, сколько весит весь кодируемый текст сообщения. Для этого достаточно вес символа алфавита умножить на количество символов в тексте. При подсчете количества символов в сообщении следует не забывать, что знаки препинания, а также пробелы – это тоже символы и они весят столько же, сколько и буквы.

Например, при условии, что каждая буква кодируется одним байтом, для текста, «Ура! Наступили каникулы.» информационный объем определяется умножением 8 битов на 24 символа (без учета кавычек). Произведение 8 * 24 = 192 бита – столько весит кодируемая фраза. В переводе на байты: 192 бита разделить на 8 получим 24 байта.

Эта схема работает и в обратной задаче. Пусть информационное сообщение составляет 2 килобайта и состоит из 512 символов. Необходимо определить мощность алфавита, используемого для кодирования сообщения.

Решение: Сначала целесообразно 2 килобайта перевести в биты: 2 * 1024 = 2048 (бит). Затем объем информационного сообщения делят на количество символов: 2048 / 512 = 4 (бит), получают вес одного символа. Для определения мощности алфавита 2 возводят в степень 4 и получают 16 – это мощность алфавита, то есть количество символов, используемых для кодирования текста.

Что мы узнали?

Одним из способов определения величины информационного сообщения является алфавитный подход, в котором любой знак в тексте имеет некоторый вес, обусловленный мощностью алфавита. Минимальной единицей измерения информации является бит. Информацию можно также измерять в байтах, килобайтах, мегабайтах.

Источник