что такое аддитивная температурная поправка
Аддитивные и мультипликативные погрешности
Аддитивной погрешностью называется погрешность, постоянная в каждой точке шкалы.
Мультипликативной называется погрешность, линейно возрастающая или убывающая с ростом измеряемой величины.
Различать аддитивные и мультипликативные п. легче всего по полосе погрешностей.
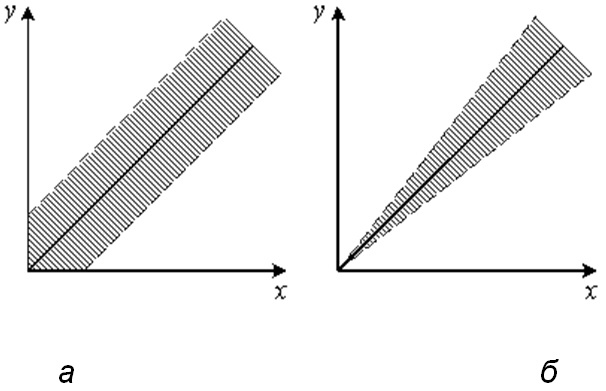
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной п. (рис. а). Иногда такую п. называют погрешностью нуля. Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и п. называется мультипликативной (рис. б). Ярким примером аддитивной п. является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной п.
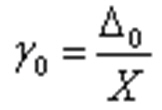
Для мультипликативной п.:
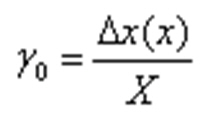
Абсолютная величина погрешности для обоих типов может быть выражена одной формулой:
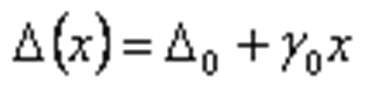
Относительная погрешность с учетом вышесказанного выражается:
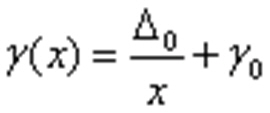
и, при уменьшении измеряемой величины, возрастает до бесконечности. Приведенное значение погрешности возрастает с увеличением измеряемой величины:
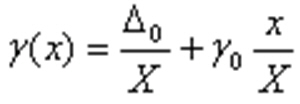
ЧИТАТЬ КНИГУ ОНЛАЙН: Метрология, стандартизация и сертификация: конспект лекций
НАСТРОЙКИ.
СОДЕРЖАНИЕ.
СОДЕРЖАНИЕ
А. С. Якорева, В. А. Бисерова, Н. В. Демидова
Метрология, стандартизация и сертификация: конспект лекций
ЛЕКЦИЯ № 1. Метрология
1. Предмет и задачи метрологии
С течением мировой истории человеку приходилось измерять различные вещи, взвешивать продукты, отсчитывать время. Для этой цели понадобилось создать целую систему различных измерений, необходимую для вычисления объема, веса, длины, времени и т. п. Данные подобных измерений помогают освоить количественную характеристику окружающего мира. Крайне важна роль подобных измерений при развитии цивилизации. Сегодня никакая отрасль народного хозяйства не могла бы правильно и продуктивно функционировать без применения своей системы измерений. Ведь именно с помощью этих измерений происходит формирование и управление различными технологическими процессами, а также контролирование качества выпускаемой продукции. Подобные измерения нужны для самых различных потребностей в процессе развития научно—технического прогресса: и для учета материальных ресурсов и планирования, и для нужд внутренней и внешней торговли, и для проверки качества выпускаемой продукции, и для повышения уровня защиты труда любого работающего человека. Несмотря на многообразие природных явлений и продуктов материального мира, для их измерения существует такая же многообразная система измерений, основанных на очень существенном моменте – сравнении полученной величины с другой, ей подобной, которая однажды была принята за единицу. При таком подходе физическая величина расценивается как некоторое число принятых для нее единиц, или, говоря иначе, таким образом получается ее значение. Существует наука, систематизирующая и изучающая подобные единицы измерения, – метрология. Как правило, под метрологией подразумевается наука об измерениях, о существующих средствах и методах, помогающих соблюсти принцип их единства, а также о способах достижения требуемой точности.
Происхождение самого термина «метрология» возводя! к двум греческим словам: metron, что переводится как «мера», и logos – «учение». Бурное развитие метрологии пришлось на конец XX в. Оно неразрывно связано с развитием новых технологий. До этого метрология была лишь описательным научным предметом. Следует отметить и особое участие в создании этой дисциплины Д. И. Менделеева, которому подевалось вплотную заниматься метрологией с 1892 по 1907 гг… когда он руководил этой отраслью российской науки. Таким образом, можно сказать, что метрология изучает:
1) методы и средства для учета продукции по следующим показателям: длине, массе, объему, расходу и мощности;
2) измерения физических величин и технических параметров, а также свойств и состава веществ;
3) измерения для контроля и регулирования технологических процессов.
Выделяют несколько основных направлений метрологии:
1) общая теория измерений;
2) системы единиц физических величин;
3) методы и средства измерений;
4) методы определения точности измерений;
5) основы обеспечения единства измерений, а также основы единообразия средств измерения;
6) эталоны и образцовые средства измерений;
7) методы передачи размеров единиц от образцов средств измерения и от эталонов рабочим средствам измерения. Важным понятием в науке метрологии является единство измерений, под которым подразумевают такие измерения при которых итоговые данные получаются в узаконенных единицах, в то время как погрешности данных измерений получены с заданной вероятностью. Необходимость существования единства измерений вызвана возможностью сопоставления результатов различных измерений, которые были проведены в различных районах, в различные временные отрезки, а также с применением разнообразных методов и средств измерения.
Следует различать также объекты метрологии:
1) единицы измерения величин;
2) средства измерений;
3) методики, используемые для выполнения измерений и т. д.
Метрология включает в себя: во—первых, общие правила, нормы и требования, во—вторых, вопросы, нуждающиеся в государственном регламентировании и контроле. И здесь речь идет о:
1) физических величинах, их единицах, а также об их измерениях;
2) принципах и методах измерений и о средствах измерительной техники;
3) погрешностях средств измерений, методах и средствах обработки результатов измерений с целью исключения погрешностей;
4) обеспечении единства измерений, эталонах, образцах;
5) государственной метрологической службе;
6) методике поверочных схем;
7) рабочих средствах измерений.
В связи с этим задачами метрологии становятся: усовершенствование эталонов, разработка новых методов точных измерений, обеспечение единства и необходимой точности измерений.
Очень важным фактором правильного понимания дисциплины и науки метрология служат использующиеся в ней термины и понятия. Надо сказать, что, их правильная формулировка и толкование имеют первостепенное значение, так как восприятие каждого человека индивидуально и многие, даже общепринятые термины, понятия и определения он трактует по—своему, используя свой жизненный опыт и следуя своим инстинктам, своему жизненному кредо. А для метрологии очень важно толковать термины однозначно для всех, поскольку такой подход дает возможность оптимально и целиком понимать какое— либо жизненное явление. Для этого был создан специальный стандарт на терминологию, утвержденный на государственном уровне. Поскольку Россия на сегодняшний момент воспринимает себя частью мировой экономической системы, постоянно идет работа над унификацией терминов и понятий, создается международный стандарт. Это, безусловно, помогает облегчить процесс взаимовыгодного сотрудничества с высокоразвитыми зарубежными странами и партнерами. Итак, в метро логии используются следующие величины и их определения:
1) физическая величина, представляющая собой общее свойство в отношении качества большого количества физических объектов, но индивидуальное для каждого в смысле количественного выражения;
2) единица физической величины, что подразумевает под собой физическую величину, которой по условию присвоено числовое значение, равное единице;
3) измерение физических величин, под которым имеется в виду количественная и качественная оценка физического объекта с помощью средств измерения;
4) средство измерения, представляющее собой техническое средство, имеющее нормированные метрологические характеристики. К ним относятся измерительный прибор, мера, измерительная система, измерительный преобразователь, совокупность измерительных систем;
5) измерительный прибор представляет собой средство измерений, вырабатывающее информационный сигнал в такой форме, которая была бы понятна для непосредственного восприятия наблюдателем;
6) мера – также средство измерений, воспроизводящее физическую величину заданного размера. Например, если прибор аттестован как средство измерений, его шкала с оцифрованными отметками является мерой;
7) измерительная система, воспринимаемая как совокупность средств измерений, которые соединяются друг с другом посредством каналов передачи информации для выполнения одной или нескольких функций;
8) измерительный преобразователь – также средство измерений, которое производит информационный измерительный сигнал в форме, удобной для хранения, просмотра и трансляции по каналам связи, но не доступной для непосредственного восприятия;
9) принцип измерений как совокупность физических явлений, на которых базируются
Погрешность измерений. Классификация
Погрешность средств измерения и результатов измерения.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.
Статическая и динамическая погрешности.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Систематическая и случайная погрешности.
Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.
Причинами возникновения систематических составляющих погрешности измерения являются:
Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.
Погрешности адекватности и градуировки.
Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.
Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.
Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.
Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.
Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
Аддитивные и мультипликативные погрешности.
Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:
– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).
Истинное значение поправки и ее модели
В реальном завершенном измерительном процессе погрешность свидетельствует только о возможном рассеянии измеренных значений, которые можно приписывать измеряемой величине.
Оценить некоторые составляющие систематической погрешности можно только в результате метрологической деятельности путем физического моделирования измерительного процесса с использованием эталонов, установок, воспроизводящих рабочие условия измерений, или математическим моделированием и только путем вычислений. Такое вычисленное при моделировании отклонение показаний от какого-либо опорного значения называется поправкой к показанию (измеренному значению) или просто поправкой. Опорным значением, например, могут служить следующие: эталонное значение в нормальных условиях; показание СИ в нормальных условиях при оценивании влияния величины, значение по референтной МИ.
На рисунке 12 изображена числовая ось измеряемой величины В, на которой показано измеренное значение и эталонное значение измеряемой величины, оценка суммарной аддитивной поправки и ее погрешность.
| В |
| Оценка поправки |
| Погрешность поправки |
| Измеренное значение величины В |
| Эталонное значение величины В |
| Допускаемая погрешность СИ |
Рис. 12 – Графическое отображение поправки и ее погрешности
на числовой оси в рабочих условиях
Суммарная аддитивная поправка равна сумме всех оцененных аддитивных поправок в нормальных и рабочих условиях. Суммарная мультипликативная поправка равна произведению всех оцененных мультипликативных поправок в нормальных и рабочих условиях.
Поправка к показаниям прибора является метрологической характеристикой, но не является погрешностью измерений в вероятностном смысле. При физическом моделировании измерений, например, в результате калибровки СИ, ее значение всегда определено с погрешностью и она сама является случайной величиной.
Процесс моделирования измерений отличается от реального измерительного процесса тем, что моделируется измерение величины, значение которой заведомо известно с высокой точностью. При математическом моделировании оно задается точно, а при физическом моделировании обязательно используется эталон, допускаемая погрешность которого меньше допускаемой погрешности рабочего СИ.
Истинное значение поправки как «разность между истинным и измеренным значением величины» определить невозможно. Его рассматривают как абстрактный параметр математической модели измерительного процесса. Напомним, что такое значение ранее принималось за погрешность измерений «по определению», но только с обратным знаком. Некоторые специалисты иногда пользуются этим определением и фактически истинное значение поправки ошибочно принимают за погрешность.
Физическое моделирование измерений выполняют при метрологических исследованиях средств измерений (при калибровке и поверке) в процессе метрологической деятельности с целью анализа качества будущих измерений и выявления поправок к показаниям приборов, хранящих ранее переданную единицу величины.
Как уже упоминалось, коррекцию показаний СИ выполняют на основе двух типов поправок, определяемых по формулам (3) и (4).
Аддитивная поправка – это разность между значением величины, воспроизведенным эталоном, и показанием прибора, хранящего ранее переданную единицу, или разность между показанием прибора в нормальных условиях, и его показанием при измерении той же величины в рабочих условиях.
Аддитивная поправка 

Опорным может быть значение, базирующееся на научных принципах, аттестованное (эталонное, приписанное, экспериментальное) значение, расчетно-экспериментальное значение и даже среднее арифметическое значение (в отсутствие эталона). Опорное эталонное значение обычно воспроизводится стандартным образцом состава и свойства вещества (материала).
Поправка всегда имеет конкретный знак или плюс, или минус. Она добавляется к измеренному значению величины со своим знаком. Не следует«поправку»называть«оценкой систематической погрешности измерений с обратным знаком». Если усилия на определение поправки уже затрачены,
то имеет смысл использовать её для коррекции показаний прибора с целью повышения показателей точности при представлении результата выполненных измерений.
Математическая трактовка поправок к показаниям и погрешностей измерений основана на теории вероятностей, теории множеств и математической статистике в предположении, что измерения могут быть повторены сколь угодно много раз. Моделирование погрешности возможно только в том случае, если предположить, что истинное значение поправки к каждому измеренному значению величины в любой момент времени известно.
Обычно поправки к показаниям СИ оцениваются и вводятся отдельно по каждой существенно влияющей величине. Реже оценивают одновременное воздействие двух и более влияющих величин.
В самом общем случае модель поправки описывает поведение истинного значения поправки к измеренному значению величины во времени и может быть представлена в виде функции времени q(t). Ее рассматривают как случайный процесс и представляют в виде суммы трех составляющих, каждая из которых может быть обусловлена действием нескольких различных источников погрешностей [9]:

Систематическая составляющая qs(t) представляет собой нестационарную случайную функцию постоянной или инфранизкочастотной поправки. Систематический сдвиг измеренного значения относительно истинного как бы изменяется («плавает») во времени. Периоды изменения составляющих систематической поправки значительно больше времени, необходимого для проведения измерения, поэтому такую поправку условно принимают постоянной.
Составляющая 


Эффективное использование рассмотренной модели поправки к измеренному значению величины возможно только при известном частотном спектре ее составляющих. На практике часто случайную составляющую поправки представляют в еще более упрощенном виде, а именно в виде случайной величины.
Таким образом, систематические и случайные эффекты в процессе определения поправки присутствуют всегда, и в дальнейшем будем рассматривать их независимыми от времени. В итоге рабочая модель поправки выглядит как:

Истинное значение поправки к измеренному значению параметра модели объекта в реальном измерительном процессе всегда неизвестно. Именно поэтому погрешность поправки рассматривается как вероятностная характеристика. Нас интересуют только границы интервала, в котором могло бы оказаться истинное значение поправки с заданной вероятностью. Следует помнить, что модель поправки, представленная формулой (33), является сильно упрощенной (не зависимой от времени) и близка к реальности только на момент ее определения. В действительности поправка будет меняться во времени и эти изменения следует учитывать, по крайней мере, при оценке показателей неопределенности на момент выполнения измерений.
Дата добавления: 2018-06-01 ; просмотров: 575 ; Мы поможем в написании вашей работы!




